CustomWriting Service On Demand
If you are a student struggling with the start or completion of an essay, you are exactly at the right time and place. We know how difficult it can be to provide an excellent paper without mistakes, citation issues, and complete structure. Our writers can help you with any writing level, subject, and essay type. Read on to see what are the benefits of using our professional essay writing service:
What essays can I get?
You can get any academic subject you must cover for school, college, or university. Custom Writing can provide various essay types, reflective journals, coursework, dissertations, editing, personal statement essays, presentations, school debates, and other types required in USA colleges. At the same time, we can provide professional writing assistance with many academic subjects, including but not limited to:
- English.
- Psychology.
- Business Management and Marketing.
- History and Anthropology.
- Law.
- Healthcare and Medical Sciences.
- Fashion Studies.
- Data Management and Analysis.
- Social Sciences.
- Education.
At the same time, we are ready to provide you with an interdisciplinary approach. If you need to combine several subjects simultaneously for your task or a college project, we can easily assist you. All you have to do is share your instructions with one of our experts.
Benefits of using our professional essay writers
Some benefits include talking directly, dealing with a native English speaker, already having proofreading and editing services, and receiving special suggestions as you discuss things. Our custom essay writing services also provide formatting and help with citations. Likewise, we can assist you if you are not managing your deadline or seek urgent writing or editing help. Approaching our academic services online, you receive:
- Direct communication with a chosen expert to eliminate communication issues.
- Professional editing and proofreading.
- Formatting, styling, and citation assistance.
- A wide coverage of essay types and academic writing levels.
- Writers with the highest qualifications are trained for quality work and respect.
- Handling urgent orders in as little as 4 hours.
- Affordable paper prices that will fit within your students’ budget.
- Free revisions and refunds guarantee financial safety.
- Confidentiality and a fully legit essay writing service.
- 24/7 customer support assistance.
Moreover, our paper service provides you with a free plagiarism-checker tool that you can use to verify originality. Since we do not use any pre-written material, we guarantee a high level of originality and zero plagiarism issues.
How to buy an essay on our website?
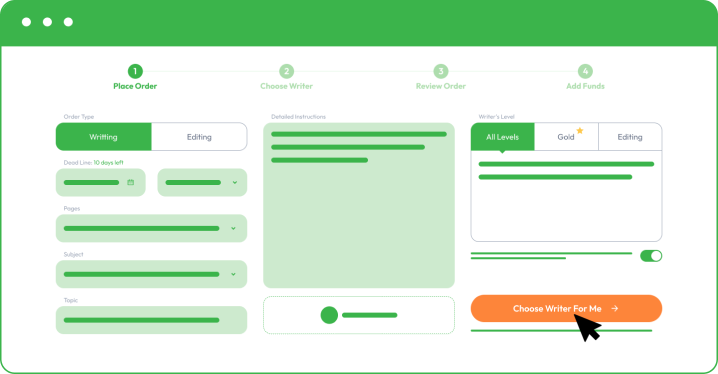
You must register and follow our instructions by sharing your order details as you place an order. The more information you share, the better we can assist you and meet your academic and personal objectives.
As you place your order with Custom Writing, you must provide the following information:
- Your subject and essay title.
- Upload instructions and comments from your college professor.
- Share formatting, deadline, and number of pages.
- Specify additional paper instructions.
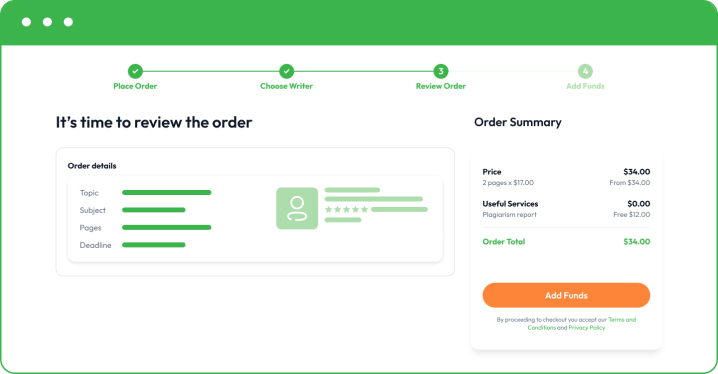
- Make a small deposit to allow your writer to start writing. Your funds will remain safe in your account, and you only release the rest when you are happy with the final essay.
By choosing a different writer’s level, you may receive better results, especially if you are aiming for a dissertation or a complex coursework task. It will come with a little addition to the final paper price, but you receive access to the top 50 or top 20 best writers in your chosen field.
Once you are happy with the final paper, you can buy custom essay and pay for the rest. Remember that we also offer free revisions to bring things to perfection. If you need to correct something or add a minor part, feel free to let your writer know directly or get in touch with our customer support.
Why should I use Custom Writing Service?
The most important is direct contact with an expert, which helps eliminate various mistakes. The second aspect is our originality and plagiarism-free work. We can provide free revisions to avoid minor mistakes and make things perfect. As an experienced team that offers high-quality and affordable prices, we know how to make you happy!
If you cannot cope with your college essays alone, you should not worry because we know what it feels like! Don’t be afraid because you are not dealing with risks as you work with a legitimate academic research company. Since you are here, you need immediate help and the best essay writing service. We are here for you and ready to offer guidance with one of the school subjects. Our team at CustomWriting is ready to help you achieve success with any written task.
If you need editing, we guarantee that we can bring things to perfection and help you submit your project on time without any pitfalls or delays on our side. Remember that if you cannot cope, you simply have to place your order with our high-quality essay writing service. Even if it’s early in the morning or late at night, do not hesitate to ask for help, as we shall immediately reply and assist you!